|
Koko länsinaapurien väittely oli itse asiassa engelsmannien
syytä. Herra nimeltään Alan Bramson (F.R.Ae.S, M.B.A.E.,
M.B.A.C.) kirjoitti ruotsiksi käännetyssä artikkelissaan
nostovoiman syntyvän yksinkertaisesti siitä, että ohittaessaan
siiven ilma joutuu kulkemaan siiven kaarevamman yläpinnan yli ikään
kuin kiertotietä, jonka vuoksi virtausnopeuden yläpinnalla
tulee kasvaa ja sitä kautta (Bernoullin lain mukaan) paineen yläpinnalla
pienetä. Tämä alipaine aiheuttaa sitten nostovoiman.
Vastaavan voiman syntyä voi hänen mukaansa havainnollistaa
esimerkiksi laittamalla lusikka kupera puoli edellä hanan alle
virtaavaan veteen, jolloin virtaus itse asiassa imee lusikkaa sisäänsä,
sen sijaan että työntäisi pois, kuten äkkinäinen
voisi olettaa. Sitä, miksi virtausnopeuden tulee kasvaa yläpinnalla
kiertotietä kulkiessaan, ei Bramson kerro.
Kuva
1. Ylä- ja alapintojen pituusero.
Moisesta teoriasta suivaantui ainakin kaksi ruotsalaista sen verran,
että he ehtivät kirjoittaa vastineensa jo heti seuraavaan
lehteen. Molemmat kehottavat unohtamaan koko Bernoullin lain ja perustelevat
nostovoiman syntyä sillä, että siipi yksinkertaisesti
taittaa virtausta alaspäin ja tämän vastavoimana, Newtonin
3. lain mukaan, syntyy nostovoima. Kiihtynyt virtaus siiven yläpinnalla
ei synnytäkään alipainetta, vaan päinvastoin: alastaittamisen
yhteydessä syntyvä alipaine siiven yläpinnan takaosalla
kiihdyttää virtausta siiven yläpinnalla.
Tästä
alkoi useassa ko. julkaisun numerossa jatkunut todellinen teorioiden
taistelu, johon osallistui lentäjiä, insinöörejä
sekä insinöörilentäjiä eri puolilta Ruotsia.
Bramson puolusti Bernoullin lakiin pohjautuvaa kantaansa ja vertasi
siipeä venturiputken puolikkaaseen. (Ilman virtausnopeushan kiihtyy
venturiputken kurkussa, koska massavirran tulee säilyä. Kun
virtauspoikkipinta-ala kurkussa pienenee, kasvaa virtausnopeus, sillä
kokoonpuristumattomassa virtauksessa putken poikkipinta-ala kertaa virtausnopeus
= vakio. Bernoullin laista seuraa suoraan, että staattinen paine
kurkussa pienenee kun virtausnopeus kasvaa.)

Kuva
2. Venturiputki. Virtaussuunta kaikissa kuvissa vasemmalta oikealle.

Kuva 3. Perinteinen Bernoullin lakiin ja venturiputkiteoriaan perustuva
nostovoiman syntyteoria.
Bramsonin mukaan siiven yläpinnalla tapahtuu sama ilmiö kuin
venturiputkessa ja nostovoima syntyy siis yläpinnan ja alapinnan
välille syntyvästä paine-erosta. Olisi kuitenkin ollut
mielenkiintoista kuulla hänen mielipiteensä siitä, kuinka
entisaikojen koneet lensivät – niissähän oli myös
kovera siiven alapinta ja hyvin ohut profiili. Hidastuuko virtaus profiilin
alapinnan etuosalla virtaputken laajenemisen, eli massavirran säilymislain
perusteella? Vai kiihtyykö se kuten yläpinnallakin joutuessaan
kiertämään koveraa alapintaa pitkin pidemmän lenkin
kuin sen alapuolella oleva suorempaan menevä virtaus…?
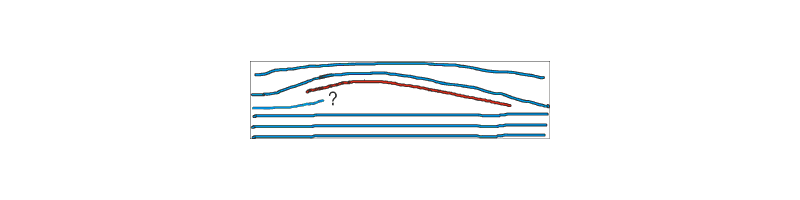
Kuva 4. Mitä tekee virtaus ohuen profiilin alapinnalla?
Mitä sitten tapahtuu yksittäiselle ilmamolekyylille siiven
eri puolilla?
Bramsonin esittelemä teoria sanoo, että kun ilma lähtee
kiertämään siipeä sen kummaltakin puolelta, tulee
eri puolilla olevien ilmapartikkeleiden olla yhtä aikaa jättöreunalla.
Koska yläpinnan partikkelilla on pidempi matka jättöreunalle,
ohittaa se siiven suuremmalla nopeudella kuin "parinsa" alapinnalla,
jonka vuoksi ylä- ja alapinnan välille syntyy Bernoullin lain
perusteella nostovoiman aiheuttava paine-ero.
Teoria muuttuu mielenkiintoiseksi esimerkiksi silloin, kun telineet
ovat alhaalla: jos alapinnalla olevia partikkeleita jää telinekuiluun
pyörimään, niin jääkö silloin osa yläpintaa
etenevistä partikkeleista odottamaan alapinnalle jumiin jääneitä
parejaan?

Kuva
5. Jääkö yläpinnan virtaus odottamaan alapinnalle
jumiin jäänyttä pariaan
ollakseen samaan aikaan jättöreunalla?
Ruotsalainen oppositio ampui Bramsonin väitteitä kovilla.
Eräs lentotekniikan diplomi-insinööri käski heittämään
sorsaa koko Bernoullin lailla. Ei sillä, etteikö kyseinen
laki pätisi kokoonpuristumattomassa virtauksessa, siis alle Machin
luvun 0.3, mutta sillä ei hänen mukaansa voi perustella nostovoiman
syntyä. Itse asiassa hän väittää, että
tavallisen pikkukoneen siiven yläpinnan tulisi olla 1,6 kertaa
alapintaa pidempi, jotta paine-ero kasvaisi kyllin suureksi aiheuttamaan
siivestä saatavan nostovoiman pienellä kohtauskulmalla.
Lisäksi hän heittää mielenkiintoisen kysymyksen:
Maavaikutuksessa syntyy siiven jättöreunan ja maanpinnan väliin
eräänlainen kurkku. Bernoullin lain ja hänen mukaansa
pitäisi tässä syntyä nostovoimaa pienentävä
alipaine. Todellisuudessahan maavaikutus kasvattaa nostovoimaa.
Tässä vaiheessa keskusteluun tulivat mukaan ilman hitausvoimat.
Hitautensa vuoksi siiven alapinnalla oleva ilma ei pysty kiertämään
siiven terävää jättöreunaa, vaan jatkaa suoraan
matkaansa. Tämä tarkoittaa siis sitä, että mikäli
profiililla on kohtauskulmaa ja/tai käyryyttä, ilma kääntyy
jättöreunalla alaspäin ja tämän ilmaan kohdistetun
voiman vastavoima on nostovoima.
Toki tässä yhteydessä siiven pinnalle syntyy paine-eroja,
mutta syypäänä ei ole kyseisen lekoinsinöörin
mukaan Bernoullin laki, vaan juuri se, että ilma ei pääse
kiertämään siiven yläpinnalle. (Toivottavasti vastineen
kirjoittaja tarkoittaa tässä yhteydessä Bernoullin lailla
yksinomaan Bramsonin esittämää venturiputkiteoriaa, sillä
kyllä itse Bernoullin laki pätee koko ajan. Se, mitä
tässä ehkä kyseenalaistetaan, on ilman kiihtyminen yläpinnalla
sen vuoksi, että yläpinnan pidemmän matkan vuoksi ilma
etenee siellä nopeammin ehtiäkseen yhtä aikaa alapuolen
ilman kanssa jättöreunalle.)Lopulta peliin puuttui myös
ammattiaerodynaamikko. Hänkin toi esiin hitausvoimat, mutta edellisen
lisäksi myös eri näkövinkkelistä, sillä
hän liitti ne keskipakoisvoimiin (oik. keskihakuvoimat).
Ajatuksena oli, että siiven yläpintaan kohdistuu alipaine
siiven käyryyden/kohtauskulman aiheuttamien keskipakovoimien vaikutuksesta
ja samalla periaatteella alapinnalle ylipaine.
Tässä
vaiheessa nostovoiman syntyteoria ei ollutkaan enää niin selkeä
juttu. Bernoullin laki oli ainakin joidenkin mielestä hyljätty
ja yhtä äkkiä puhuttiinkin keskipakoisvoimista. Seuraavassa
kirjoittajan yritys koostaa nämä kaikki fysiikan lait yhdeksi
kokonaisuudeksi: Nostovoiman synty - yksi esitystapa.
Tuulitunnelikokeiden perusteella ilmamassa kulkee nostovoimaa synnyttävän
siiven yläpinnalla alapinnan virtausta nopeammin, ohittaen jättöreunan
alapinnan virtausta edellä, mutta samalla nopeudella. Etumatka
johtuu siitä, että siipi kiihdyttää virtausta yläpinnalla,
kun taas virtaus alapinnalla hidastuu tai ainakin nopeutuu vähemmän.
Kiihtymisen yläpinnalla aiheuttaa yläpinnan kaarevuus ja virtauksen
puristuminen profiilin etuosalla. Tämä taas johtuu siitä,
että ilmaa ei pääse kiertämään alapinnalta
jättöreunan ympäri yläpinnalle; jättöreunaa
kohti syntymään pyrkivä alipaine täyttyy ja virtausta
ohjautuu siiven yläpinnalle tätä vastaava määrä
jatkuvuusyhtälön perusteella. Yläpinnalla tulee tällöin
ahdasta, virtaus puristuu ja sen seurauksena kiihtyy.
Mitä enemmän kohtauskulma kasvaa, sitä suurempi osa virtausta
kulkee yläpinnan kautta ja sitä alemmas siirtyy patopiste,
eli se piste, missä virtaus törmää kohtisuoraan
profiilin etureunaan. (Vrt. esim. sakkausvaroittimen sijainti ja kulma
– sakkauskohtauskulmalla patopiste on melko alhaalla etureunalla;
sakkausvaroitin toimii kun patopiste siirtyy varoittimen alapuolelle).
Nyt voidaan ottaa se kuuluisa Bernoullin laki pureskeltavaksi. Profiilin
pinnalla todella syntyy paine-eroja Bernoullin lain mukaan: yläpinnalla
virtaus siis kiihtyy ja kuristuu, eli syntyy staattista alipainetta.
Alapinnan olosuhteet taas riippuvat profiilista ja kohtauskulmasta.
Monesti alapinnallekin syntyy alipainetta, mutta vähemmän
kuin yläpinnalle, jolloin staattisen paineen nettopaine-ero on
ylöspäin.
Kuvan 4 tapauksessa käyrän profiilin alapinnalla virtaviivat
ovat harvemmassa, jolloin virtaus hidastuu ja staattinen paine alapinnalla
on vapaan virtauksen staattista painetta suurempi.
Otto Lilienthal kirjoitti jo vuonna 1895, että siiven yläpintaan
kohdistuu alipaine siiven käyryyden/kohtauskulman aiheuttamien
keskipakovoimien vaikutuksesta ja samalla periaatteella alapinnalle
ylipaine. Keskipakovoimat taas aiheutuvat ilman massahitaudesta –
aivan kuten kurvaavassa linja-autossa tekee mieli ottaa pystytangosta
tukea, ettei lennä lattialle oman (massa)hitautensa vuoksi. Näiden
keskipakoisvoimien aiheuttamien paine-erojen vaikutuksesta syntyvät
sitten nopeuserot siiven ylä- ja alapinnan välillä (Bernoullin
lain mukaan).
Otto Lilienthalin keskipakovoimateoria on juuri sopiva sekoitin tähän
väliin sotkemaan muutenkin vaikeaa asiaa.
Teoria saattaa kuulostaa melkoiselta utopialta, mutta pohditaanpa asiaa
hieman bussiesimerkin avulla: Istut bussissa pystytangon oikealla puolella
ja bussi kurvaa oikealle. Otat kiinni tangosta ja työnnät
itseäsi tangosta poispäin pysyäksesi pystyssä. Teet
käytännössä samaa kuin ilmapartikkeli siiven alapinnalla
joutuessaan muuttamaan suuntaa sen pintaa myötäillessään.
Tämä siis silloin, kun profiililla on nollanostokohtauskulmasta
poikkeava positiivinen kohtauskulma. Sitten bussi kurvaa vasemmalle.
Joudut roikkumaan tangossa keskipakovoimaa vastaan välttääksesi
kaatumasta oikealla puolellasi istuvan juopon syliin. Vedät siis
tankoa itseesi päin, aivan kuten kupera siiven yläpinta "vetää"
sen ohi kiitäviä ilmapartikkeleja itseensä päin
ja päinvastoin.
Jos ilma ei seuraisi siiven pintaa, syntyisi jättöreunalle
periaatteessa tyhjiö, sillä ilmaa ei pääse kiertämään
alapuolelta tilalle.Bussiesimerkissä alipainetta vastaa kurvaavassa
bussissa kämmenessä tuntuva veto ja ylipainetta taas ranteessa
tuntuva puristus, kurvaussuunnasta riippuen. Kuva 6. Ylä- ja alapinnan
virtausten nopeuserot. Yläpinnalla virtaus on kiihtynyt alapinnan
virtausta enemmän ja mennyt sen vuoksi ohi. Musta viiva kuvaa patopisteeseen
törmäävää virtaviivaa.
Oleellinen
tekijä nostovoiman synnyssä on virtauksen suunnan muuttaminen,
joka aiheuttaa erisuuruisia kiihtyvyyksiä ja paine-eroja siiven
pinnalla. Tämä taas ei ole mahdollista ilman siiven (riittävän)
terävää jättöreunaa, sillä terävän
reunan vuoksi virtaus ei pääse alapinnalta kiertämään
yläpinnalle, jolloin virtaus pakotetaan kulkemaan käyrää
reittiä kohtauskulmaa omaavan profiilin ohi. Kuten edellä
mainitsin, virtauksen patopiste siiven etureunalla siirtyy alas siten,
että usein jopa etureunan alapuolella olevaa ilmaa nousee siiven
edellä sen yläpinnalle. Siiven takana taas virtaus jättää
alaspäin kulmassa olevan jättöreunan siten, että
sillä on komponentti alaspäin. Eli siipi nostaa ilmapartikkeleita
ensiksi ylös ja painaa sitten alas, jolloin ilma tekee siiven kohdalla
käytännössä mutkan alaspäin.
Kuten edellä kehitetty bussiteoriakin todistaa, liittyy mutkan
tekoon aina voimia eli tässä tapauksessa siis nostovoimaa.

Kuva 7. Jos alapinnan virtaus kykenisi kiertämään jättöreunan,
olisi virtauskenttä seuraavanlainen => ei nostovoimaa.
Musta
viiva kuvaa patopisteiden paikkaa etu- ja jättöreunalla sekä
virtauksen suunnan muutosta.

Kuva 8. Todellinen tilanne: alapinnan virtaus ei pysty kiertämään
jättöreunaa, virtauksen suunta muuttuu => nostovoimaa.
Musta viiva kuvaa patopisteiden paikkaa etu- ja jättöreunalla
sekä virtauksen suunnan muutosta.
Huom.
patopiste siirtyy alaspäin myös etureunalla.
Sivulla http://www.grc.nasa.gov/WWW/K-12/airplane/wrong3.html voi käydä
katsomassa hienoa interaktiivista livevisualisointia virtauksen käyttäytymisestä
siipiprofiilin ympärillä.
Matemaattisesti virtauksen kääntymistä siiven ympärillä
mallinnetaan lisäämällä vapaaseen virtaukseen ns.
sirkulaatio, G. Sirkulaatio on "yksinkertaisesti" nopeusvektorin
viivaintegraali virtauskentässä olevaa suljettua ympyrää
pitkin, ja kun tuon ympyrän sisälle jää nostovoimaa
synnyttävä siipiprofiili, saa sirkulaatio nollasta poikkeavan
arvon.
Nostovoiman
kaavaksi tulee sitten L’=roVoG, missä L’ on nostovoima
per kärkivälin mittayksikkö, ro on vapaan (tulevan) virtauksen
tiheys ja Vo on vapaan virtauksen nopeus (tosi-ilmanopeus). Sirkulaation
SI-yksikkö on m2/s, tiheyden kg/m3 ja nopeuden m/s, eli L’:n
yksiköksi tulee kg/s2, joka on sama kuin voiman yksikkö Newton
(kg-m/s2) jaettuna mittayksiköllä eli metrillä. Siis,
matemaatikon näkökulmasta lentokone lentää yksinkertaisesti
siksi, että L’=roVoG!
Ostin joulunpyhinä sellaisen viinipullon suulle taivutettavan ohuen
kiiltävän muoviläpyskän, jolla estetään
viinin valuminen pitkin pullonkaulaa ja pöytäliinan tahriintuminen.
Totesimme pöytäseurueen kanssa yksimielisesti, että vehje
toimii: tällä kertaa ei tipan tippaa valunut pitkin pullonkaulaa
tai tippunut liinalle. Tosin aerodynamiikkaan perehtymätön
pöytäseurani ihmetteli hieman kommenttiani, kun sanoin, että
lentokone lentää itse asiassa juuri saman ilmiön ansiosta
kuin miksi kyseinen ohut teräväreunainen läpyskä
pullon suulla pelasti pöytäliinan.
TEKSTI:
RISTO PAJUNIEMI
Yllä oleva teoria perustuu kotimaiseen ja ulkomaiseen akateemiseen
lentotekniikan opetukseen sekä kirjallisuuteen,
ja on sen pohjalta muodostunut kirjoittajan henkilökohtainen näkemys.
Kirjoittaja on koulutukseltaan lentotekniikan DI ja ammattilentäjä.
|
|